扩展功能
文章信息
- 孔维宝, 董妙音, 李万武, 牛世全, 曾家豫
- KONG Wei-Bao, DONG Miao-Yin, LI Wan-Wu, NIU Shi-Quan, ZENG Jia-Yu
- 从莫诺方程谈起——生物类本科专业教学中3 个相似方程的探讨
- Cogitation from monod equation: discussion of three similar equations in biological undergraduate teaching
- 微生物学通报, 2015, 42(8): 1599-1602
- Microbiology China, 2015, 42(8): 1599-1602
- 10.13344/j.microbiol.china.140906
-
文章历史
- 收稿日期: 2014-11-13
- 接受日期: 2015-01-15
- 优先数字出版日期(www.cnki.net): 2015-03-17
在生物、制药和化工类相关专业课程的学习中,“微生物”和“微生物工程”课程中有关微生物细胞生长动力学中的莫诺方程(Monod equation)[1, 2],“生物化学”和“酶工程”课程中有关酶促反应动力学方程——米氏方程(Michaelis-Menten equation)[3, 4],“物理化学”、“生物分离工程”、“制药分离工程”课程中有关吸附与吸附分离中的Langmuir等温吸附方程(Langmuir equation)[5, 6, 7],这3个方程虽然应用于不同的学科领域,各自代表不同的参数,解决不同的学科问题,但是三者的数学本质却一致。比较学习、探讨上述3个形似方程,除了为教师在教学中提供启发学生思路,为学习三门相关课程的学生提供类比关联学习方法的同时,也提示了一种联想发散式的教学思路,尤其是在涉及定量问题的教学探讨和科学研究中。
将3个学科领域中各自重要的3个方程联系起来,比较分析挖掘出其表现的客观过程本质上的相似性,最终得出相似的数学模型,利于学生(包括教师)更丰富深刻地理解这种从客观事实的表现探究其本质机理,在探究过程中总结其内在规律,寻求定性或定量的可能研究方法,最终建立符合其客观本质的数学模型,从而使某类问题的研究有了一般化的公共数理基础。同时这种比较探讨也说明了数学在自然科学研究中的重要意义和积极作用。下面就上述3个方程的比较学习和启发做一探讨。
1 莫诺方程(Monod equation)莫诺方程用来描述当化合物作为唯一碳源时,化合物的降解速率。当培养基中不存在抑制细胞生长的物质时,用莫诺方程来表示细胞的生长速率与基质浓度关系。
| $\mu = \frac{{{\mu _{\rm{m}}}S}}{{{K_{\rm{s}}} + S}}$ | (1) |
式中:μ:比生长速率;μm:最大比生长速率;Ks:半饱和常数,比生长速率为最大比生长速率一半时的基质浓度;S:生长的基质浓度。
莫诺方程基于3个基本假设:(1) 细胞的生长为均衡式生长,因此描述细胞生长的唯一变量是细胞的浓度;(2) 培养基中只有一种基质是生长限制性基质,而其他组分为过量,不影响细胞的生长;(3) 细胞的生长视为简单的单一反应,细胞得率为一常数。
在同一种基质中,Ks为常数,Ks通常很小;当基质浓度很高时,Ks可以忽略不计,即Ks+S=S,此时,μ=μm,细胞以最大比生长速率生长。对数生长期细胞的生长就属于这种情况。当基质浓度很低时,Ks+S=Ks,则μ=μmS/Ks,此时,比生长速率与基质浓度成正比,基质浓度变化引起比生长速率变化迅速。
将莫诺方程取倒数可得:1/μ=1/μm+Ks/μm·S或S/μ=S/μm+Ks/μm。
这样通过测定不同限制性基质浓度下细胞的比生长速度,就可以通过回归分析计算出莫诺方程的两个参数μm和Ks。
2 米氏方程(Michaelis-Menten equation)米氏方程是由德国化学家米夏埃利斯(Michaelis)和门藤(Menten)归纳的表示酶促动力学基本原理的数学表达式,此方程式表明了底物浓度与酶反应速度间的定量关系,表示一个酶促反应的起始速度(v)与底物浓度(S)关系的速度方程,是在假定存在一个稳态反应条件下推导出来的。
| $\nu = \frac{{{V_{\rm{m}}}[S]}}{{{K_{\rm{m}}} + [S]}}$ | (2) |
式中:v:反应速率;Vm:最大比生长速率;Km:米氏常数,反应速率为最大反应速率一半时的底物浓度;[S]:底物浓度。
在酶促反应中,在低浓度底物情况下,反应相对于底物是一级反应;而当底物浓度处于中间范围时,反应(相对于底物)是混合级反应。当底物浓度增加时,反应由一级反应向零级反应过渡。
Km值的物理意义为反应速度(v)达到1/2 Km时的底物浓度(即Km=[S]),单位一般为mol/L,Km只由酶的性质决定,而与酶的浓度无关。可用Km值鉴别不同的酶。当底物浓度非常大时,反应速度接近于一个恒定值。在曲线的这个区域,酶几乎被底物饱和,反应相对于底物S是个零级反应。就是说再增加底物对反应速度没有什么影响。反应速度逐渐趋近的恒定值称为最大反应速度Vm。
Km和Vm的意义如下:
(1) 当v=Vm/2时,Km=[S]。因此,Km等于酶促反应速度达最大值一半时的底物浓度。
(2) Km可以反映酶与底物亲和力的大小,即Km值越小,则酶与底物的亲和力越大;反之,则越小。
(3) Km可用于判断反应级数:当[S]<0.01Km时,ν=(Vm/Km)[S],反应为一级反应,即反应速度与底物浓度成正比;当[S]>100Km时,ν=Vm,反应为零级反应,即反应速度与底物浓度无关;当0.01Km<[S]<100Km时,反应处于零级反应和一级反应之间,为混合级反应。
(4) Km是酶的特征性常数:Km的大小只与酶的性质有关,而与酶浓度无关。因此,在一定条件下,某种酶的Km值是恒定的,因而可以通过测定不同酶(特别是一组同工酶)的Km值,来判断是否为不同的酶。
(5) Km可用来判断酶的最适底物:当酶有几种不同的底物存在时,Km值最小者,为该酶的最适 底物。
(6) Km可用来确定酶活性测定时所需的底物浓度:当[S]=10 Km时,ν=91% Vm,为最合适的测定酶活性所需的底物浓度。
(7) Vm可用于酶的转换数的计算:当酶的总浓度和最大速度已知时,可计算出酶的转换数,即单位时间内每个酶分子催化底物转变为产物的分 子数。
(8) Km和Vm的测定:主要采用Lineweaver-Burk双倒数作图法和Hanes作图法。
3 Langmuir等温吸附方程(I型等温线)等温吸附方程是指在一定温度下,溶质在吸附剂上的吸附平衡关系是指吸附达到平衡时,吸附剂的平衡吸附质浓度q与液相游离溶质浓度c之间的关系。该理论常用于生物物质或药物的吸附分离过程。当温度一定时,吸附量与浓度之间的函数关系称为吸附等温线。
| $q = \frac{{{q_{\rm{m}}}c}}{{{K_{\rm{d}}} + c}}$ | (3) |
式中:q:吸附剂的平衡吸附质浓度;qm:饱和吸附容量;Kd:吸附平衡的解离常数;c:液相中的游离吸附质浓度。
该方程的单分子层吸附理论在很多情况下可解释溶质的吸附现象。其理论要点为:(1) 吸附剂上具有许多活性点,每个活性点具有相同的能量;(2) 活性点上只发生单分子层吸附;(3) 每个吸附点只能吸附一个分子,并且被吸附的分子间无相互 作用。
4 3个方程的相似性分析与学习启示从上述分析可以看出,莫诺方程、米氏方程和等温吸附方程这3个方程虽然应用于不同的学科领域,各自的参数代表不同的函数意义,用来解决不同的学科问题,但是三者的数学本质却相通。
建立参数模型在于确定已知模型中的各个参数,并通过理论分析总结出参数模型。同样,在生物学的研究中,利用某些定量关系的数学公式可建立具体的数学模型,再通过建立的数学模型来研究一些抽象的动态过程,定性或定量的角度来刻画实际问题,并为解决现实问题提供精确的数据或可靠的指导。
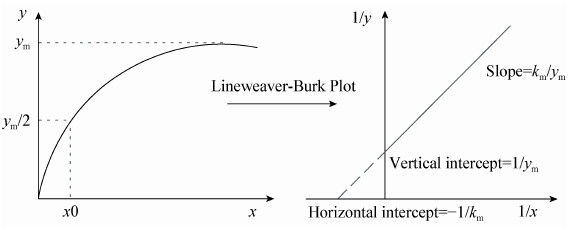
因此,在建立方程时,首先要求解方程中的参数。米氏方程是利用数学的理论,推导出来的公式。在米氏方程中,直接从起始速度对底物浓度的图中确定Km和Vm值是很困难的,因为曲线接近Vm是个渐进过程。为了方便地测得准确的Km和Vm值,可把米氏方程的形式加以变换,使它成为直线方程,然后用图解法求出Km和Vm值。利用Linewearver-Burk作图法(双倒数作图法)将米氏方程式两侧取双倒数,得到下面的方程式:
<| $\frac{1}{v} = \frac{{{K_{\rm{m}}}}}{{{V_{\rm{m}}}}} \times \frac{1}{{\left[ S \right]}} + \frac{1}{{{V_{\rm{m}}}}}$ | (4) |
|
| 图 1 双倒数作图法 Figure 1 Double reciprocal plot |
同理,莫诺方程是在试验数据基础上,通过统计其规律而得出的经验公式。在求解莫诺方程时,同样可以用双倒数作图法来求解方程中的参数μm和Ks。将莫诺方程式两侧取双倒数,得到方程式:1/μ=Ks/μm·S+1/μm,然后通过测定不同限制性基质浓度下,细胞的比生长速度,就可以通过回归分析计算出莫诺方程的两个参数μm和Ks。
在Langmuir等温吸附方程(I型等温线)的求解过程中,若将式(3)两侧取双倒数,改写成1/q=Kd/qm·c+1/qm,然后以1/q对1/c作图,依然可以得到一条直线,求解可得:横轴截距=−1/Kd,纵轴截距=1/qm,斜率=Kd/qm,可由斜率和截距求得Kd和qm的值。
因此,三者的常数均可采用类似于米氏方程中两个常数(Km和Vm)的求解方法来求解,例如采用Linewearver-Burk作图法(双倒数作图法)、Hames-woolf作图法或Endie-Hofstee作图法均可求解图 1中的km和ym。
建立这种数学模型,可以很方便地探究、挖掘具体事物的本质及关系,最终以直观的数学模型的形式将其中的规律揭示出来,使复杂的问题本质化、简洁化,甚至将其一般化,使某类问题的解决有了共同的程序与方法。由此看来,通过深入学习其中某一个方程的推导过程、参数含义、常数求解等,触类旁通,就可轻松掌握3个在不同课程中的重要知识点,达到不同关联知识的融会贯通。另外,在相关专业学习和科学研究中,遇到类似的过程问题,可以尝试采用上述的方法建立数学模型和方程,来解决理论研究和实际生产中的具体问题。
| [1] | Shen P. Microbiology[M]. Beijing: Higher Education Press, 2006: 136-138 (in Chinese) 沈萍. 微生物学[M]. 北京: 高等教育出版社, 2006: 136-138 |
| [2] | Yao RH, Zhou SS. Process Principle of Microbial Engineering[M]. Guangzhou: South China University of Technology Press, 2005: 149-152 (in Chinese) 姚汝华, 周世水. 微生物工程工艺原理[M]. 广州: 华南理工 大学出版社, 2005: 149-152 |
| [3] | Wei SZ. Biochemistry[M]. Beijing: China Light Industry Press, 1996: 137-141 (in Chinese) 魏述众. 生物化学[M]. 北京: 中国轻工业出版社, 1996: 137-141 |
| [4] | Chen SW. Enzyme Engineering[M]. Beijing: Science Press, 2008: 12-14 (in Chinese) 陈守文. 酶工程[M]. 北京: 科学出版社, 2008: 12-14 |
| [5] | Zhang XP. Synchronous Counselling and Exercises Complete Solution for Physical Chemistry[M]. Beijing: China Mining University Press, 2007: 294-295 (in Chinese) 张霄鹏. 物理化学同步辅导及习题全解[M]. 北京: 中国矿业 大学出版社, 2007: 294-295 |
| [6] | Tian RH. Bioseparation Engineering[M]. Beijing: Science Press, 2008: 161-162 (in Chinese) 田瑞华. 生物分离工程[M]. 北京: 科学出版社, 2008: 161-162 |
| [7] | Ying GQ. Drug Separation Engineering[M]. Hangzhou: Zhejiang University Press, 2011: 108-109 (in Chinese) 应国清. 药物分离工程[M]. 杭州: 浙江大学出版社, 2011: 108-109 |
 2015, Vol. 42
2015, Vol. 42